Categories
article project management

Understand stakeholders better for the best chances of success

Two Problems

Someone has given you a new shiny project to do, so you’ve got a problem that needs a solution. Thing is now you have two problems, the easy one is probably the shiny project, the harder one is managing the stakeholders.

To avoid poor project outcomes some stakeholders (like managers) will just want information, some are providing resources to the project and some have to be managed to prevent them derailing or threatening the project’s success.

First Steps in Stakeholder Analysis

As with anything in project management the first step is always to make a list that captures something of the problem you’re facing and from that we can pull out some germ of truth to help us figure out what to do next.

So in your list gather:

  • The stakeholder’s name, email, handle, etc.
  • The stakeholder’s role or relationship to the project, and any groups you can identify
  • The stakeholder’s project power vs project interest (optional)

We’ll explore these topics in a bit more depth now.

Roles

When ordinary people become stakeholders in a project some of their expectations as stakeholders differ on account of the different roles that the stakeholder plays. For example, the managing director of your firm will have a different point of view on the project to the lead developer, which will be different again than the point of view of the firm’s clients.

Some key roles to look out for in your project are:

  • Sponsor – the person who wants this project and whose word is final on the project. This person can clear the path of potential issues around and above the project (if necessary). Ideally it’s just one person, if it’s more than one try to make it one because it removes a potential political hurdle when dual sponsors have different views.
  • Subject Matter Experts (SMEs) – these are easy to spot, they’re the people that you can consult on more technical aspects or specifics. They may or may not be people that contribute directly to the project, but having an SME agree with you (or you agreeing with them!) is never a bad way to be.
  • Project Managers – you might think you’re the project manager, but often there are other people on the periphery who will exert control over the project without explicitly being given authority to do so. It’s good to identify the people that might do this, if only to communicate what the lines of responsibility actually are.
  • Project Team – the workers, this might include you but generally it’s anyone who will work on the project in whatever capacity. If you have lead engineers or support staff it’s useful to identify this too (so that when you share this information other people can use it like a directory).
  • Externals – so if you have external stakeholders to your organisation then the chances are their opinion is quite important. This is likely because they’re clients or they will be beneficiaries or affected by the project in some way. They will probably not contribute much to the project but you need to understand them. If you have more than one type of external stakeholder, record that as well.

Power vs Interest (optional)

There are many things you can do with stakeholder analysis. They’re all designed to give you insight into what people might expect. Power vs interest is a very common and reasonably useful way, but there are plenty of others, each with their own strengths and benefits.

To be honest there’s no absolute need for this but you might do it for two reasons:

  1. It’s sometimes quite revealing to formulate opinions on people’s expectations through this lens.
  2. It can be quite fun!

Before you make the list though, be careful to consider who might see your list. Even though you may try to be truthful/accurate you may find the people you have captured information on disagree with your categorisations. Which can be both embarrassing and frustrating, so consider whether you will make two lists. One to communicate and share with the other stakeholders, and one that is just for you to understand their motivations.

If you do decide to try it, it’s very straight forward. For each of your stakeholders mark them out of 10 in terms of their power/influence on this project (0=no power or influence, 9=very powerful/influential) and then mark them again for their interest (0=no interest, 9=very interested).

Then plot them on a scatter chart, where they appear on that diagram will influence how you communicate with them.

  • Bottom left – no power/no interest – you don’t want too many people in this quadrant if you do you might have a problem delivering the project.
  • Top left – lots of power/no interest – keep these people up-to-date they have the ability to derail your efforts.
  • Bottom right – no power/lots of interest – hopefully the junior members of your project team is in here somewhere.
  • Top right – lots of power/lots of interest – hopefully your sponsor, PM and more senior project team members are in here.
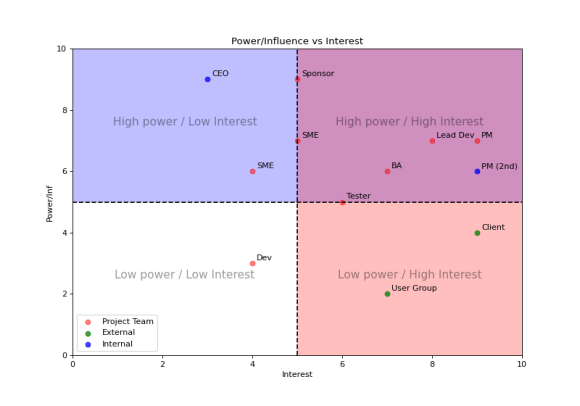
Power and influence vs interest graph showing four quadrants to fully understand your stakeholders better

These things are very subjective, so when you plot it first time it probably won’t feel quite right. You might have scored some of the people on different aspects of power/interest (since there are many). So tweak it a bit until it feels like you can justify the diagram as a whole.

Putting it all together

You’ve got your list, you’ve plotted your scatter diagram what now? Well if you’re lazy like me you might leave it there. You’ve done the analysis, you know more now than you did at the start, but some more useful things you could do with your stakeholder analysis are:

  • Communicate On It – I’ve hinted at this already, but it’s very helpful for everyone to know what their role is on a project. It helps set their expectations from you and your expectations of them. I’d personally just share the version with just names and roles in it at the start of the project. If questions arise at this stage it’s good to get them out in the open.
  • Plan From It – a lot of the people in your stakeholder analysis are likely to be key resources in your project. Having them, their diaries and their availability easily accessible in your project folder makes everything a bit simpler.
  • Reorganise the Team – if after doing the power vs interest analysis you decide that your team isn’t balanced, and you have scope to do it, use the analysis to reorganise the team or make some substitutions. To be honest though I’ve rarely had this luxury.
  • Communicate With It – a lot of successful project management is about communication. If you understand the stakeholders then you can tailor the communications to suit the stakeholders. For example the sponsor is employing you to handle the details, so high level progress and issues will probably be fine for them – but it depends on their level of interest. The SMEs and externals probably just like to know high level progress but you might phrase it differently for each audience. Finally, the project team probably want short term detailed plans. So, come up with a small suite of reports and decide who gets what report and use your analysis as a guide to the distribution and content.
Categories
python

The Low Tech Secret Santa

We’re all Santas now

Secret Santa, if you didn’t know, is a gift-giving game that seeks to reduce the overall burden of buying gifts to a single gift for one person instead of a gift for every person. It also, usually, place limits on the spend which prevents people over or under buying.

For most people the solution to running a ‘Secret Santa’ is pretty simple but it’s worth repeating the process for clarity:

  1. Write the names of your friends/family/colleagues on scraps of paper;
  2. Fold the names of the Santas up and put them in your (hacking!) hat;
  3. Each Santa takes it in turn to pull out a name from the hat;
  4. If any Santa gets themself as their match return to step 2;
  5. Buy gifts and exchange them sometime later.

The ‘secret’ part refers to the fact that no-one should know, who is their Santa or any other pairing. It usually also means that you never find out who bought you your gift, but that part is optional and there is often plenty of fun to be had discussing it afterwards.

Trouble at the North Pole

Problems start to arise when you can’t get all of the people who want to participate in the draw in the same physical room at the same time.

Your first thought might be (like mine was) “well surely there’s an app for that where you tap in all the names and the app privately sends out the matches”.

And you’d be right, there are plenty. But what if the person who is remote to the draw doesn’t have a usable mobile device or use email? I know this is hard to believe but these people do exist. And believe me, I have tried to fix this problem by fixing the bigger problem but progress has been slow. So, for now at least, apps and email are out.

Your second thought might be (like mine also was) “I could just use snail mail to send out the draw to the remote persons”. But the problem with this is that there is a chance, if one person or more is remote then one or more of those remote persons get themselves in that draw. This would reset the draw and mean we’d need to do it over.

So obviously I can fix that by sending out multiple draws and selecting the first one that works. Right? So the question then becomes how many trial draws do I need to be certain of a valid gift giving extravaganza?

99% Confident Santas

So how many draws do we need, for us to be 99% certain that those pre-draws will be successful and give us valid pairings? This problem description is a special case of the Binomal distribution which has the following general formula to find the probability of getting exactly r successes from n trials with probability p: 

nCr . p^{r}.(1-p)^{n-r}

But what we actually want is the probability of 1 or more successes, which is the logical opposite statement of the probability of no successes at all. When you substitute that into the Binomial formula it simplifies to:

1-(1-p)^n

But what is p?

One way to estimate it is if you write out by hand the set of valid outcomes for different sizes of groups we can get an idea of what sort of values p takes.

nValidPermutations (n!)p (approx)
1010
2120.5
3260.333
49240.375
Table of probabilities of success in a trial of n

It turns out that this number oscillates as the group size increases but it looks like it’s converging to somewhere just above 1/3. In my case I really want to know p for a group size of 6 so a computer is needed to brute force that answer. This is of course in the absence of a specific insight on the nature of the ‘Santa sequence’ which would allow me to calculate the valid outcomes without brute force, but more on that in Part 2.

Turns out that in Python you can write an expression to do that in a one-liner but for clarity I’ve split it onto 3 lines.

>> import itertools, numpy, math
>> santa = numpy.array([1,2,3,4,5,6])
>> sum([1 for z in itertools.permutations(santa) if math.prod(z-santa) != 0])
265

What this does is to produce a Python iterable object which has all the different permutations of this array [1, 2, 3, 4, 5, 6]. If we use the order of the array to indicate the pairing (i.e. the first item corresponds to the first santa, the second item to the second and so on) then [1, 2, 3, 4, 5, 6] is clearly the worst draw since every Santa is paired with themselves.

By using itertools permutations then, we can use this abstraction to represent all possible draws of six Secret Santas as a list of arrays (spoiler the length of this list is the same as 6! which is 720).

But how do we check for a valid draw? One cheap way to know if a draw is valid is to subtract the index of each Santa from the index in the permutation given. If the draw is invalid the subtraction will put one or more zeros in the array, and when you find the product of that array it will be zero if it is invalid and non-zero if it is valid.

Doing this gives the new information we need, that there are 265 valid draws with a group of six people. Which is a p of about 0.3681.

Solved it! Now We Have Two Fails.

So now we want to know how many draws are needed to be 99% confident that one of the draws will succeed. We could simply use our simplified Binomial ‘at least one success’ formula to calculate the probability of success after n trials and then stop when we hit 99% but where is the fun in that?

The ScipPy optimiser is the sledge-hammer we need for this nut, it just needs us to rearrange our equation so that the answer we’re looking for would give zero when put into a Python function.

>> from scipy.optimize import fsolve
>> fsolve(lambda x: 1-(1-265/720.)**x-0.99, 1)
array([10.03406063])

So we need about 10 draws to be confident that it will only go wrong one time in a 100. But, when you think about the mechanics of putting together 10 independent Santa draws and stuffing them in the Royal Mail that feels like a lot of work.

Not only that, there is a much bigger chance that I will mess something up when putting the draws together and it results in a failed draw for a purely human reason (as opposed to a mathematical one).

Another Approach

Then I hit on a slightly different approach which is just a step further towards a generalised approach that could allow us to do as many draws as we want, but probably only when the number of Santas is low.

I now know how to generate all the permutations, and how to identify valid drawings easily, and also how many valid drawings there are (i.e. 265). This number is small enough that perhaps the easiest thing to do, in this case, is to send all Santas a personalised list that gives them their pairing in one of the 265 possible valid outcomes. Then all I need to do is to send out those personalised lists via post and email to all the Santas.

On the date of the draw then someone simply selects a random number from 1-265 and everyone reads their Santa off the list. Sure, as the organiser, I could find out who has which pairing but that’s not really a concern because I really don’t want to know. So I just won’t look.

Conclusion

I ran this process as a trial (to make sure everyone ‘got it’) and then we did it for real on 31st October 2021. I think it worked fine, but we might not really know until the gifts are given. Lol.

This puzzle raised a lot of other questions that I haven’t delved into in this post. In the next post I’ll provide a link to the code that generated the draw sheets that I sent out to my fellow Santas (in-case someone wants to use what I’ve done to run their own Secret Santa) but I’ll also delve into the sequence for p to see if we can answer questions like:

  • What does p converge to?
  • What if the number of Santas is bigger than 10?

But until then I’ve got some shopping to do. 🙂

Categories
shaders

WebGL for noobs: How to make a square circle

So as I mentioned in the last post I’ve been messing around with OpenGL shaders. To be honest I know next to nothing about shaders or OpenGL but it’s fun to take a look at these things to try and gain some intuition about how they work. Hopefully by doing so I’ll be able to build complex and interesting shaders of my own, but I’m getting ahead of myself.

So let’s start with something simple, a shader of concentric circles. It’s based upon a somewhat more fascinating shader, but there’s more than enough to talk about with just this simple example.

It turns out that the shader code to draw an animated set of concentric colourful circles requires just 2 lines. Well that’s not quite true you could write it one line if you wanted. But that’s also not quite true, there are a lot of lines of WebGL to get the two lines below to do something in the first place. But once those lines of code are done the bit that makes just the drawing is effectively one formula that can be compiled on the GPU.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {   
  vec2 u = vec2(fragCoord/iResolution.xy-.5) * vec2(1.,iResolution.y/iResolution.x);
  fragColor = vec4(fract(length(u)*4. + vec3(0.,1.,2.)/3. + iTime/16.),1.);
}

You’ll notice that there aren’t any loops in the code and that’s because what we’re writing is conceptually the centre of a loop managed by WebGL that will get executed once for every pixel we want to shade.

Too Shadey

I should explain a little bit first. In OpenGL there are a few types of shader that form part of the rendering pipeline. But, for the purposes of this series of posts the OpenGL pipeline is a black box and we’re only really interested in the fragment shader that can be constructed in such a way as to supply window input co-ordinates and produce an associated colour for that co-ordinate.

Co-ordinate Systems

A WebGL fragment shader receives pixel co-ordinate as natural numbers where the origin (0,0) is at the bottom left of the canvas. Therefore the first thing many shaders do is to convert those co-ordinates into a new set where the origin is in the centre of the screen and the range of x and y is some set of values that makes the subsequent maths a bit simpler.

How they do this varies, and is not super interesting, but being able to extract the range from the domain of input values is often important for making sense of what happens next. A lot of OpenGL math involves vector and matrix math. For this example it’s not too important to understand this more deeply than a vec2 is a pair of x,y points.

vec2 u = vec2(fragCoord/iResolution.xy-.5) * vec2(1.,iResolution.y/iResolution.x);

I loved my Atari ST it was the third personal computer I owned (preceded by a ZX81 and a ZX Spectrum) and it had a whopping 320×200 resolution with a mighty 512 colours. All on the same screen at the same time! Amazing. So if our device has that resolution then we simply calculate the range of y by substituting in the display resolution.

\tfrac{0}{200}- \tfrac{1}{2} * \tfrac{200}{320} \leq y \leq \tfrac{200}{200} - \tfrac{1}{2} * \tfrac{200}{320}

When you simplify you get the new range of x,y values which reveal that the range of values and that the pixels have been corrected for the aspect ratio to keep them square.

-\tfrac{1}{2} \leq x \leq \tfrac{1}{2},  -\tfrac{5}{16}\leq y \leq \tfrac{5}{16}

Normally, it’s not magic

The final part, and where the magic actually happens, is in the following code segment. The part that provides the ‘circularity’ is the call to length this is because this tells us how far our point in the plane is from the origin (which we placed in the centre). Length is the same as the linear algebra vector operation ‘normalise’ (or norm), that in two dimensions is also simply the old high school favourite Pythagoras.

fragColor = vec4(fract(length(u)*4. + vec3(0.,1.,2.)/3. + iTime/16.),1.);

If we imagine a slice through our circles along the line y=0 then length(u) is equal to x since clearly:

length(x,0)=\sqrt{x^2+0^2}=x

By removing a dimension we can now reason about what the rest of the calculation must do. Since our length will be x then when we scale it by the constant 4 we will end up with x in the range of between -2 and 2. We then add this to the vector:

\begin{pmatrix}\tfrac{0}{3} & \tfrac{1}{3} & \tfrac{2}{3}\end{pmatrix}

It is this step that essentially gives the circles their colour change. We now have three different ranges for the different colour channels and so we will end up with the following:

\begin{matrix}-2 \leq r \leq 2 \\ -1\tfrac{2}{3} \leq g \leq 2\tfrac{1}{3} \\ -1\tfrac{1}{3} \leq b \leq 2\tfrac{2}{3}\end{matrix}

However OpenGL only shows colours in the range of zero to one (if the value is greater than one it is capped at one) and this is the final step. We take the fract in order to give us just the fractional part of the calculation so our values for each channel will range between zero and one. This gives us a type of oscillation where each colour channel will rise steadily towards full saturation but then drop sharply drop to zero afterwards. The key is that each channel will do this on a slightly different period and this is what gives us the candy type colours. In order to visualise this a bit more clearly I’ve made a plot showing how the three channels vary when y=0.

Time to wrap it up

This has been a long post, but we’re not quite done. The part of the formula that gives the circles their animation is the addition of iTime/16. Since iTime is the amount of seconds since the shader began this will have the effect of gently pushing each peak of the RGB channel toward the centre on every frame. I should also point out that it significantly changes the ranges of the colour channels (RGB) prior to the call to fract but because we call fract it makes no difference to the final output range of those channels of between 0 and 1.

This has been a pretty long post. There were a lot of basic things to explain before actually getting to the point. Subsequent posts will be a lot shorter I hope so that we can focus on the interesting stuff!

Categories
graphics shaders

WebGL for noobs: The Shadey Student

In the last post, I wrote about getting wowed by WebGL fragment shader hacks. They are simultaneously fascinating and baffling, how can something seeming so simple give rise to such magic?

… an uninformed public tends to confuse scholarship with magicianry…

Foundation and Empire – Isaac Asimov (1952)

It seems then that I am the uninformed public. Again.

Over the years I’ve come to realise that trying to explain something to others is the way to really understand something. It’s an approach that has been broadly given the name: ‘The Feynman Technique’. Which is to say, I think, it’s something Feynman did in his teachings at CalTech. Rather than a bite sized self-help method developed by him to sell stocking filler books. But all props to the Feynman legend, the system works and so I’m going to aim to gain understanding by trying to explain what’s going on under the hood here on this blog. Note that I’m not a mathematician and so there are probably better explanations of how some of this works than mine, most likely what you need, if you want the good stuff is here.

Armed with all the heavy-hitting celebrity ‘thinking’ quotes that I need to motivate, me I’ve set out on this endeavour. The first step of which is creating tools for the job. Whilst shadertoy.com is the bomb and my inspiration, there are two reasons I’ve decided not to use it for this:

  1. I would need to publish my shaders on shadertoy.com in order to embed them here. What I intend to do in explaining is a little too trivial for what I think shadertoy.com should be used for;
  2. Shadertoy.com seems a bit slow, probably because it’s really popular! Better that I don’t add to that burden (although three page views a week isn’t going to hurt them!) but also better to have control over the content. IMHO.

Therefore I’ve created a little WebGL Javascript embedding tool. Based upon Mozilla’s great WebGL tutorials and inspired by shadertoy.com. It’s stripped down to simplify what needs to be done but the shaders I create with it should be compatible with shadertoy.com when, and if, I do want to publish something.

Finally the last part of the stack is having a graphing tool that I can use to embed custom plots into these pages to explain the functions that are used in the shaders – because this is where the magic is. For that I’m using Python 3.8 with Matplotlib. It’s not the prettiest but it’s definitely more than good enough.

Let the fun begin.

Categories
article graphics shaders

New Toys

I have been interested in computer graphics for a long time but never really interested enough to make some positive steps toward it. Like a lot of people, I have tried to get a basic app working in OpenGL or DirectX but never really got very far. It was all a bit intimidating.

However things have changed. These days, on DirectX, there are a load of fantastic tutorials on the internet, as well as seriously helpful libraries. If you’re interested in getting some physics working there’s a few good books and often the content is backed up with source code. For WebGL (which is a flavour of OpenGL) there’s great tutorials to help, and really cool insights into how it works.

There’s quite a lot to take in before you can really grok what the graphics pipeline does, whatever API flavour you chose. It was whilst trying to figure out how shaders work that I stumbled across some stunning examples of what is possible. What I didn’t realise, at first, is that the examples I was looking at are simply fragment shaders.

If you don’t know how 3D graphics works you might say ‘so what?’. But let’s just say it’s not the easy route to getting 3D computer graphics done – not to me anyway. The mathematics involved looks in a lot of ways harder, but the programming looks way easier. Programming this way is mostly declarative, there’s no bonkers API and there are far fewer loops because the magic is in the power of the GPU and the shader loop.

My only problem is that shadertoy.com doesn’t quite work how I want it to. For one thing it keeps timing out (guess they need more funds, so I added some through Patreon), but that aside I wanted a bit more control over the shader and how it can be embedded. Partially for this blog but also to learn a bit more WebGL.

That happened two weeks ago. I’ve been messing around trying to get something working for this site and making some embeddable shaders that I can embed directly here. I think I’m almost there …

Categories
article

Server timed out. Rebooting.

TL;DR: The hat is back!

It has been over 10 years since I last wrote something on this blog. Some usual life stuff happened that I won’t trouble you with. The rain fell, but mostly, the sun shone.

After 5 years of letting the site rot I’ve just spent the best part of 2 days getting it back up, it’s had:

  • OS upgrade;
  • WordPress upgrade;
  • but most importlanty a new logo!

5 years of rot has gifted me about 4,000 accounts created by SEO spam-bots so in a fit of rage I deleted all registered accounts. As far as I can tell there is very little spam (if any) on the site, which brings me to my next point.

I’ve disabled comments. I realise, a blog without comments isn’t really a blog at all. But the problem is, as the number of spam posts increase it becomes painful to moderate and so I don’t. Turning off comments is fairer to potential commenters, who might write a comment and never have it published. At least I’m saving you some time.

I’m looking into alternatives, but so far in all the usual places. Perhaps I’ll find something that addresses my problems with spam that doesn’t involve Google. We’ll see.

After all the work of getting the site up I felt like I should probably write something. I’ve been doing some interesting (to me) hobby research into knowledge engineering and separately, computer graphics and shaders. Alongside my day job of project management, there’s a lot of potential topics, and perhaps some of those musings will end up right here – in the hat.

To keep the pace up, the promise I’m making myself is that new posts will be shorter. So … let’s end it there and see what happens next.

Categories
programming

Programming Like It’s 1995

Object-oriented programming, where is it now? When I was at college we learnt a little about object methods and techniques and when I left I kept reading about them. I remember in the 90s I was incensed that an employer was NOT using object methods appropriately. I EVEN read books about it. You could say I was an object fan-boy. But even I have to admit that OOP didn’t exactly deliver how I expected it would.

You may say that this is a crazy talk and that OOP was/is hugely succesful. Shark-jumping mumbo jumbo. But I might disagree. In fact, sometimes I think the object-baggage we’ve inherited is perhaps as much a hinderance as it is a help. The wake-up call came a few months ago when I realised that almost every piece of code that I’m in contact with these days makes only limited use of object-techniques.

Before I talk about all the ways that OOP is dead let me be clear in the ways that it is not. Because when I say OOP is mostly-dead, I mean it is mostly dead to me. In some areas OOP has delivered in spades. For example in modern OO programming languages nearly all come complete with large object libraries. This much is true. There’s objects in them-thar binaries for sure. But my code? Not so much.

Here’s all the ways I manage NOT to write truly object-oriented software:

The Task is Too Small

Some systems are just too small to develop a complex object class hierarchy for. It would be a waste of time to do so. I estimate these ‘glue’ applications could take up as much as 5% of the total LOC of a large enterprise system. It doesn’t matter whether these glue applications are written in Java or Python or Bash because really they’re just scripts. Scripts are their own thing. I would argue that the less scripts you have in your system the better you designed it because you’re not just duct-taping over the seams.

The Spreadhseets Rule

I would also estimate that some appreciable percentage of your enterprise is run entirely from spreadsheets. Whether you know about it or not. Be it phone book, accounts, trading system or stock inventory. These little beauties contain little or-no object code and are spread far-and-wide. I’ve ranted about the pervasiveness of spreadsheets before, no need to go over it again. However, as far as I know, no-one has implemented the idea of an OO spreadsheet. For that we can all be thankful.

World Wide Wasteland

Although the web does lend itself beautifully to model-view-controller, on the client side a lot of it is only markup and Javascript. Neither markup nor JS have particularly strong OO characteristics and both are hugely succesful without those OO characteristics. Indeed many WWW apps are really CRUD applications.

CRUD

The create-update-delete application is everywhere. Be it web-or-desktop. These apps are effectively database front-ends that organise the interactions between user and DB in a more user-centric way. For example in .NET there’s not much need nor desire to map your data into real-objects because the data-binding layer is phenomenally powerful at making data-bound apps quickly. There’s no support to help you map from data to objects to Infragistics. Indeed, nor should there be.

Enterprise Business Objects

JSP And this is the bit that makes me a bit sad inside. This is what OO was really meant for. I used to have arguments with business-analysts about the right object model to use and whether a method should exist in a base-class or a derived-class. But now it doesn’t seem like anyone, including me, really cares. It’s just that somewhere along the line it became a little irrelevant. Don’t get me wrong, I work with objects all the time. But they’re not really objects that were sold to me.

They’re just data-holders or as our fathers used to say: data-records.

No Methods? No Object

The thing is that to me at least, without methods on your objects there’s literally no object. If objects doesn’t respond to messages they’re just data-records transferring data to some other module that can operate on those records. Usually this other module takes the role of a controller. This, to me, sounds very similar to the programming that our fathers used to-do before C++ and Java 1.1. So much so that it’s tempting to break open my book on JSP.

I think there are two fundamental areas where objects failed to deliver.

Finance This

Firstly, whilst OO techniques are very flexible in some business domains they aren’t flexible in exactly the right ways for all business domains. I’m thinking particularly about my own area of expertise, which is financial trading systems.

The objects in trading systems tend to be difficult to compose into a meaningful hierarchy that is both expressive and not too abstract. I think ultimately this failing is because financial instruments are actually themselves models of physical events. This means that it’s straight-forward enough to construct an object-model of financial instruments. However as soon as I start innovating with my financial instruments (i.e. construct new financial models from old ones) the original object models tend to break-down pretty fast.

The Technology Stack Sandwich

The second reason is that there are too many different technologies involved in many enterprise-sized solution stacks to make consistent application of OO methods viable. What does that mean? Well this is perhaps a post in itself but essentially as soon as you are using two or more programming languages that must share objects you’re essentially entering an object-desert.

The End?

Oh no. Very definitely not. Objects are the only way to make sense of a deep-and-wide library. If the domain allows it they are the only way to go.

The surprise is that objects just didn’t deliver in the way that I thought that they might for me. Which is kind-of interesting because it suggests to me that perhaps me, and a lot of people like me, might benefit from forgetting about objects sometimes and just Programming Like It’s 1995.

Categories
windows

Using Git from behind an NTLM proxy

For some reason the Git that ships with Cygwin (v1.6.6.1) won’t do the right thing with NTLM proxies. It seems that Git uses cURL underneath and that cURL can correctly handle NTLM authentication if the options are set correctly.

However, the version of Git I have isn’t capable of passing this information through. In fact, some browsing of the issues that people have with this suggests that there is more than one part of Git that isn’t able to work correctly with NTLM. So even if you’re able to get past the initial connection you probably won’t be able to fetch any of the tree.

The solution, in full then, is to use ntlmaps to act as a proxy to the proxy. All you need to do is to download the latest version of the app from: ntlmaps. Change the config file to include your authentication and proxy details, start it up and then set the proxy to be your new local one:

git config --global http.proxy http://localhost:5865

I can confirm that it works just fine. Not only that you can use it for any app that requires NTLM authentication but does not provide full NTLM support.

Categories
lisp

The Excel Gambit


Excel screen shot of XL-Gambit
XLREPL


In the spirt of shoving Lisp where Lisp should-not-go I have jammed Gambit Scheme into Excel.

If you’re interested in trying it out you should go and get the files RIGHT NOW at GitHub. You just need to add the compiled .XLL into your add-ins and use the formula =GAMBITC(“(+ 1 1)”) in a cell of your choosing.

Please note this is a proof-of-concept. You probably shouldn’t use it for anything important, most importantly because it probably leaks like a sieve. You should also know I only really tested it on Excel 2003. It should load into Excel 2007 but I didn’t try that yet.

Why? Because it’s there, and I’m here

Why did I do it? Well the rationale behind doing this was that I wanted to write an app for Excel in Scheme. I want to do that because I think it would be vastly superior to using .NET or VBA or COM. Having spent a few hours on it I think I could definitely achieve what I set out to do but whether I’ll actually go this route in the end I’m undecided about. More on that later.

Mature like a good cheese

The Excel API, as it turns out, is … well … mature. Now I like old things quite a lot. I’m old, and I like me just fine. One consequence of age is that we get a little extra baggage on the way. This is true of Excel too.

Now, IMHO one of the more challenging aspects of programming a long-lived project is version management. Especially version management of an API. Broken backwards/forwards compatibility of those APIs could be serious impediments to a new Excel’s acceptance. Unsurprisingly then Excel has a number of APIs that have all undergone various enhancements over the years. To me though the switch from Excel 2003 to Excel 2007 was the most significant, requiring the most additional cognitive load to work with. For now, and for simplicity, I have chosen to totally deny the existence of Excel 2007. But I’m coming back to it, oh yes I am.

I Eat Pain For Breakfast

I had read a bit online about the Excel C API and found it all hugely confusing. So I bought a book thinking that that would make it clearer. Although the author does attempt to explain how you might write an Excel add-in he does it in a way that makes programming from it hard. For example, the information I need is spread all-over the book. Answering a single question about Excel’s behaviour with respect to calling the core Excel4/Excel12 function necessitates flicking between the index and more than 10 different page sections.

The reason for this is probably that Excel is really a very versatile tool which is why a lot of the world’s business (large and small :)) seem to operate their database, accounts and customer details from it. So there’s not really one track through the development process. There’s literally hundreds, limited only by your imagination!

Having said that the book in combination with the Excel 2007 SDK was sufficient to pick through the rubble and build something workable. Maybe I’ll try and produce some guides/tutorials of my own to make the topic clearer. Maybe.

On the Gambit side there’s not much more documentation than what’s on the manual HTML page to help. Like the Excel book it is also very densely populated with information. IMHO its main failing is that it could really do with having more documentation of the C macro functions. Did I ever mention that I hate C macros? Well in Gambit these undocumented C macros are effectively what Gambit Scheme is written in and you kind-of need a fairly thorough explanation of how it all fits together to be able to make an effective glue with them. I will be coming back to this later when I try and construct lists from cell ranges.

Finally I decided to do this all in MinGW rather than the more usual VC++. Whilst going this route did cost me a bit of time I’d much rather use the GCC toolchain because I understand it better.

Where-to-now

Now that I have the interpreter in Excel I will probably work on tidying it up for Excel 2007. More importantly though, I want to see if I can exploit Excel 2007’s all important multi-threading capability.

If that all works out I might use it to make a custom add-in. I will develop the app from the REPL in Emacs using Gambit Scheme. When it’s done I’ll compile it up into a standalone XLL with Gambit. That’s the plan anyway.

Let me know if you like it, or can see a use for it. Encouragement is always good.

Categories
education flash

Some Sums Sum, Sum Don’t

My eldest daughter has been getting maths homework for a year or two now. We try and do the homework together and I try and make it fun but it’s hard. It’s hard because if she doesn’t understand something by the second time I explain it, then to her I become like the teacher in Charlie Brown. Blah Blah Blah. This is especially true if when I’m explaining elementary mathematics, I make a mistake in my explanation. This happens often and only causes to confuse her royally.

And so it was with the topic of number bonds. My wife discovered, by attending a parent’s maths workshop at the school, that the children were learning that certain numbers in base 10 arithmetic are bonded. The bonds are simply as follows:

  • 1->9
  • 2->8
  • 3->7
  • 4->6
  • 5->5

It’s fairly trivial but also fairly powerful in that once you know these bonds it’s a shortcut for mental arithmetic. We, as adults, know these ‘bonds’ so well that we probably don’t even recognise that we use them. The challenge then is to teach children this trick and thereby speed up their arithmetic ability.

One of the techniques that my daughter’s school uses is to send home ‘games’ that try and reinforce the learning they have done in the class. These games usually consist of a laminated sheet of instructions, a dice or two or other simple props. Usually these games are quite good and instructive. Some times they are totally confusing because they are meant to reinforce what was learnt in class and that doesn’t come across in the instructions. You’d think that I could ask my daughter to explain ‘how’ they should be doing it. It doesn’t work. Kids just aren’t that ‘meta’, that’s why they’re so much fun.

Now I have observed both my children playing on friv and Club Penguin. They are totally immersed in the most crappy Flash apps (although I have to say that most of them are actually quite fun!). So I thought I’d try and see if I could make a Flash game that would teach a little mathematics.

A while ago an ex-colleague posted about a super-cool Flash application he’d made. From that I figured out I could download the SDK and most of what I needed for free. However I thought I’d try the 60-day trial of Flex Builder. The added comfort of Flex builder is that it’s a pre-configured Eclipse for building Flash apps, so progress is pretty smooth-and-fast. Not sure I’d spend the $299 for a personal license though. It’s not that good.

I had always thought that Flash development was complex but it turns out that it really isn’t. If you can program Javascript, then there really isn’t that much extra to learn to make it work because you can use ActionScript (which is a derivative of ECMAscript as Javascript is). The biggest difficulty I found was with laying out text. Something that HTML laps up, but turns out to be really cumbersome in Flex. I’m probably just doing it wrong.

And so the unimaginatively titled ‘Number Bonds’ was born. Enjoy.

If you’re interested in the code it’s here. It’s pretty messy though. I’ve also made a back-story-free page about ‘Number Bonds’ here.